Das perfekt verschachtelte 3D-Rätsel

Dreidimensionale Puzzles sind viel mehr als nur Denkspiele. Sie sind beeindruckende Beispiele für die vielfältigen Möglichkeiten des 3D-Drucks. Technologisch relevant ist das für elektromagnetischen Einheiten, Architektur und Robotermontage. Ein Team internationaler Computerwissenschafter:innen um den ISTA-Vizepräsidenten für Technologietransfer und Oscar-Preisträger Professor Bernd Bickel hat nun eine Toolbox veröffentlicht, mit der sich hochgradig verschachtelte Puzzles entwerfen lassen. Die Arbeit wurde auf der SIGGRAPH-Konferenz mit dem Technical Paper Award ausgezeichnet.

Verzahnte Puzzles sind verblüffende geometrische Spiele. Ihre Teile werden durch ihre geometrische Anordnung zusammengehalten, die auch verhindert, dass man sie auseinandernehmen kann. Eine spezielle Unterklasse dieser „Interlocking Puzzles“ hat dabei einen sehr hohen Schwierigkeitsgrad. Es sind mehrere Schritte nötig, um sie zu zerlegen. Und das ist eine herausfordernde Aufgabe, da man zahlreiche Konfigurationen erkunden muss, bis man einen Punkt erreicht, an dem das erste Stück freiliegt und herausgenommen werden kann. Eine noch größere Herausforderung ist aber das Design solcher Puzzles.

Ein Team von Forscher:innen der Singapore University of Technology and Design, der ETH Zürich und der École polytechnique fédérale de Lausanne (EPFL) in der Schweiz sowie des Institute of Science and Technology Austria (ISTA) stellen nun auf der SIGGRAPH-Konferenz ein Programm vor, um solche Puzzles mit der Rechenleistung von Computern zu erstellen. Der iterative und robuste Algorithmus ist für alle frei zugänglich, die ihr eigenes Puzzle entwerfen möchten. „Wir haben ein Toolkit entwickelt, mit dem sich hochgradig verschachtelte Puzzles nach den Wünschen der Benutzer:innen entwerfen lassen, einschließlich der Form, der Anzahl der Puzzleteile und des Schwierigkeitsgrads“, lädt Computerwissenschafter Rulin Chen die Community ein.

Zugehöriges Video auf YouTube ansehen

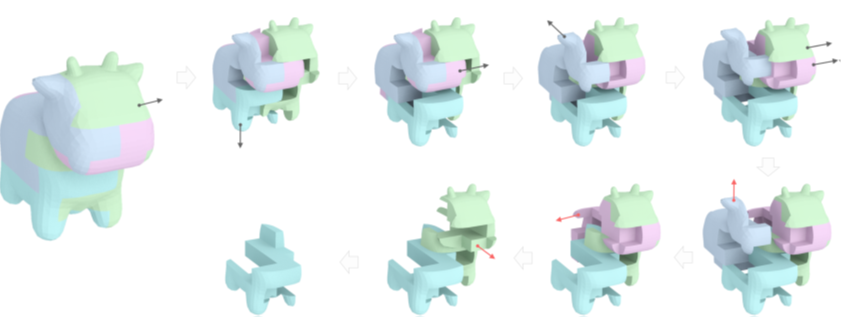
Animation von Erstellung und Lösung des Puzzles. In einer virtuellen Umgebung modellierten die Informatiker:innen die ineinandergreifenden Puzzles, die später zum Ausprobieren im 3D-Drucker gefertigt wurden. © Rulin Chen et al.

Die Lösung des Rätsels, wie man lösbare Rätsel erstellt

Stellen Sie sich vor, Ihr Lieblingstier wäre eine Eule. Das Computerprogramm würde die Eulenform als 3D-Gitter modellieren, das gleichmäßig in kleine Volumeneinheiten, so genannten Voxel, unterteilt ist (2D-Bildelemente werden bekanntlich Pixel genannt). Der Algorithmus garantiert, dass alle Puzzleteile die gleiche Größe haben und alle Voxel, die ein Puzzleteil bilden, miteinander verbunden sind. Außerdem verhindert er Konstruktionen, bei denen man ein Teil mit dem ersten Zug entfernen kann. Mit diesen Anforderungen im digitalen Hinterkopf beginnt der Algorithmus mit dem Entwerfen von Puzzleteilen innerhalb des „voxelisierten“ Gitters.

Der Algorithmus braucht nur sechs Minuten, um ein vierteiliges Kuhpuzzle mit dem Schwierigkeitsgrad 6 zu erstellen – das bedeutet, dass mindestens sechs Züge erforderlich sind, um das erste Teil zu entfernen. Für einen Würfel mit dem Schwierigkeitsgrad 27 braucht der Computer mehr als sechs Stunden.

Testlauf mit gedruckten Puzzles

Fast jede Form kann zum Puzzle werden, solange sie keine eingeschlossenen Volumina aufweist, so wie etwa Muscheln oder Bäume. Wenn das Puzzle weniger als acht Teile hat, bleibt die Komplexität des Problems und die Dauer der Erstellung überschaubar. „Natürlich funktioniert unser Projekt nicht nur in der Theorie. Wir haben verschiedene Puzzles in 3D gedruckt, um herauszufinden, wie schwierig es für Leute ist, sie zu lösen“, sagt Professor Bernd Bickel und scherzt: „Schnell war klar: die Puzzles sind echt knifflig. Und auch, dass das Eulenpuzzle mit Abstand als das niedlichste empfunden wird.“

Publikation

Rulin Chen, Ziqi Wang, Peng Song, und Bernd Bickel. 2022. Computational Design of High-Level Interlocking Puzzles. ACM Transactions on Graphics, Vol. 41, No. 4, Art. 150 (Proceedings of SIGGRAPH). DOI: 10.1145/3528223.3530071

Förderungen

DieArbeit wurde durch den SUTD Start-up Research Grant SRG ISTD 2019 148, den Schweizerischen Nationalfonds (SNF) NCCR Digital Fabrication Agreement #51NF40-141853 und den European Research Council (ERC) Grant MATERIALIZABLE-715767 finanziert.