„Drumbeats“ als mathematischer Beweis

Eine Trommel und Billard auf einem runden Tisch. Zwei Begriffe, die eigentlich wenig miteinander zu tun haben. Beide benutzt jedoch Vadim Kaloshin, Professor am Institute of Science and Technology Austria (ISTA), um eine Reihe faszinierender Fragen zu erforschen.  Wie hilft das Trommeln dabei, eine hundert Jahre alte Vermutung über Billard zu beweisen? Und wie enthüllt die Mathematik die tiefen Verbindungen zwischen diesen scheinbar disparaten Konzepten? Für seine Arbeit in diesem Gebiet erhielt er nun einen Best Paper Award.

Die Mathematik macht es möglich, die wesentlichen Eigenschaften und zugrundeliegenden Prinzipien physikalischer Systeme zu erfassen und zu beschreiben. Vor etwa hundert Jahren nutzte G. D. Birkhoff diese Fähigkeit der Mathematik, physikalische Systeme zu abstrahieren, um das Billardspiel in eine mathematische Spielwiese zu verwandeln. Dabei betrachtete er den Billardtisch als eine Begrenzung und die Kugel als eine Punktmasse, jede mit bestimmten Eigenschaften ausgestattet. So konnte er sich auf qualitative Fragen konzentrieren (zum Beispiel über die Bewegung der Bälle oder die Form des Tisches), ohne von physikalischen Details überwältigt zu werden.

Die wohl tiefgründigste Frage zum mathematischen Billard ist die Birkhoff-Vermutung – sie ist fast ein Jahrhundert alt und immer noch ungelöst. Im Wesentlichen besagt sie, dass die Begrenzung des Tisches eine Ellipse (eine regelmäßige ovale Form) sein muss, wenn die Bewegung der Kugel immer periodisch (die Kugel wiederholt den gleichen Weg) oder fast periodisch (der Weg wird mit einer gewissen Genauigkeit wiederholt) ist. In der folgenden Abbildung sind die grünen und blauen Linien Beispiele für periodische Bahnen.

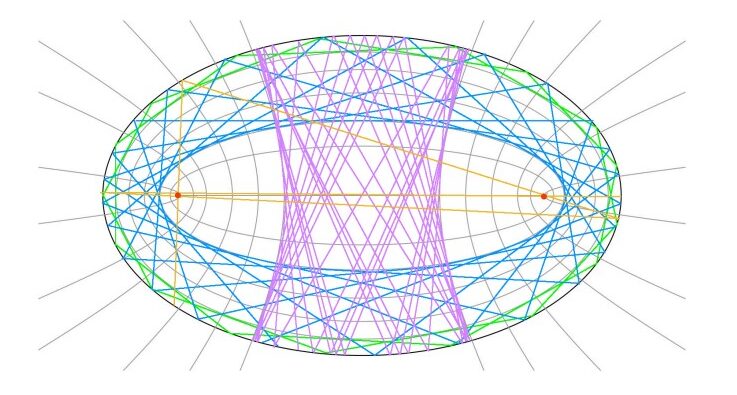
Schnell wurde klar, dass die mathematische Spielwiese deutlich mehr zu bieten hat. Billardähnliche Dynamiken kommen überall vor: Zum Beispiel in Atomen eines Gases, die sich in einem Behälter bewegen, oder Schallwellen, die sich durch einen Raum schwingen.  Auf letzteres wurde ISTA-Professor Vadim Kaloshin durch eine weitere, über hundert Jahre alte Frage aufmerksam.

„Kann man die Form einer Trommel hören?“

Im Wesentlichen geht es um die Frage, ob der Klang einer Trommel auf einzigartige Weise ihre Form definiert. Mark Kac stellte diese Frage in einer gleichnamigen Publikation aus dem Jahr 1966, ähnliche Fragen reichen sogar in das Ende des 19. Jahrhunderts zurück. „Zum ersten Mal hörte ich von dieser Frage während meiner Doktorarbeit“, erinnert sich Kaloshin. „Damals beschäftigte ich mich mit dynamischen Systemen. Bei einem sich entwickelnden System versuche ich, mithilfe der Mathematik die Dinge zu erklären, die rätselhaft sind.“ Beispiele für solche geheimnisvollen, sich entwickelnden Systeme gibt es zuhauf, von der Instabilität in den Kirkwood-Lücken im Asteroidengürtel unseres Sonnensystems und der Arnold-Diffusion – wo Kaloshin einige seiner berühmtesten Beiträge leistete – bis hin zu den Frequenzen unterschiedlich geformter Trommeln.

Kacs Frage wurde 1992 verneint, als zwei verschiedene Formen mit demselben „Klang“ gefunden wurden:

Viele damit zusammenhängende Fragen bleiben jedoch unbeantwortet. Kaloshin und seine Gruppe am ISTA erforschen, ob zum Beispiel die Verformungen einer Trommel ihren Klang verformt. „Eine der Techniken, die wir verwenden, ist die Betrachtung der Billardwege der Schallwellen“, sagt Kaloshin. „Wir haben erforscht, wie wir die Klänge von Trommeln nutzen können, um etwas über Billardwege zu ermitteln. Das heißt, wie könnten wir eine Anwendung nutzen, um etwas über die Theorie zu beweisen?“ So machten sich Kaloshin und sein Mitarbeiter daran, einen Beweis für die Birkhoff-Vermutung zu finden.

Mit einer Anwendung die Theorie zu beweisen

„Wenn es sich wie eine Ellipse anhört, dann IST es eine Ellipse“, erklärt Kaloshin. Zwar konnten Kaloshin und sein Mitarbeiter die Birkhoffs Vermutung nicht vollständig auflösen, dennoch gelang es ihnen, einen bedeutenden Fortschritt zu erzielen. Im Wesentlichen zeigen sie, dass eine Ellipse immer noch eine Ellipse ist, auch wenn sie auf eine kleine, glatte, strikt geordnete Weise deformiert wird. Wäre dies nicht der Fall gewesen, hätte dies die Birkhoff-Vermutung widerlegt. Die daraus resultierende Arbeit, die in den Annals of Mathematics veröffentlicht wurde, wird diese Woche auf dem International Congress of Basic Science in Peking mit einem Best Paper Award ausgezeichnet.

Am Ball bleiben

Im Sommer 2021 verstärkte Illya Koval über das ISTernship-Programm des ISTA die Kaloshin-Gruppe. Fasziniert von Kaloshins Vorträgen zu diesem Thema und der Beschreibung des Problems machte sich Koval an die Arbeit, um die Theorie weiter voranzutreiben. Nach einigen Wochen verallgemeinerte er Kaloshins Ergebnisse, indem er die Einschränkungen für die Wege der Billardkugeln verringerte. Koval, der inzwischen ins Doktorandenprogramm des ISTA aufgenommen wurde und sich der Kaloshin-Gruppe angeschlossen hat, ist weiterhin davon fasziniert: „Der Traum ist es, die globale Birkhoff-Vermutung zu beweisen, aber dafür brauchen wir einen neuen Ansatz“, so Koval. „Wir bleiben am Ball.“

Publikationen:  

Kaloshin, V. & Sorrentino, A. 2018. On the local Birkhoff conjecture for convex billiards. Annals of Mathematics. DOI: 10.4007/annals.2018.188.1.6 (Preprint hier verfügbar DOI: 10.48550/arXiv.1612.09194)

Koval, I. 2023. Local strong Birkhoff conjecture and local spectral rigidity of almost every ellipse. arXiv Preprint. DOI: 10.48550/arXiv.2111.12171