Ein Wörterbuch der abstrakten Mathematik

Mehrere Bereiche der Mathematik haben in völliger Isolation voneinander ihre eigenen ‚unentzifferbaren‘ kodierten Sprachen entwickelt. In einer neuen Studie, die in PNAS veröffentlicht wurde, stellt Tamás Hausel, Professor für Mathematik am Institute of Science and Technology Austria (ISTA), „große Algebren“ vor, ein mathematisches ‚Wörterbuch‘ an der Schnittstelle zwischen Symmetrie, Algebra und Geometrie, das auch die entfernten Welten der Quantenphysik und der Zahlentheorie stärker verbinden könnte.

Begriffsbestimmungen: Symmetrie und Kommutativität, von der Ästhetik zur Funktionalität

• Die Symmetrie ist nicht nur eine Frage der Ästhetik und des Gleichgewichts, sondern auch ein in allen Bereichen des Lebens immer wiederkehrendes Merkmal. In der Mathematik ist die Symmetrie eine Form der ‚Invarianz‘: Ein symmetrisches mathematisches Objekt bleibt auch bei bestimmten Rechenarten oder Transformationen unverändert.
  • Die Gruppe aller Transformationen, unter denen ein mathematisches Objekt unveränderlich bleibt, wird als ‚Symmetriegruppe‘ bezeichnet.
  • Symmetrien wie die Drehung eines Kreises oder einer Kugel können als ‚kontinuierlich‘ eingestuft werden. (Im Gegensatz dazu ist die Spiegelung eines zweiseitig symmetrischen Objekts wie die Flügel eines Schmetterlings ein Beispiel für eine ‚diskrete‘ Symmetrie.)
  • Kontinuierliche Symmetriegruppen werden mathematisch durch Matrizen – rechteckige Zahlenreihen – dargestellt, mit denen die Eigenschaften des mathematischen Objekts in lineare Algebra umgewandelt werden können.
• Kontinuierliche Symmetriegruppen werden als ‚kommutativ‘ bezeichnet, wenn die Reihenfolge der Operationen oder Transformationen keine Rolle spielt. Andernfalls sind sie ‚nicht kommutativ‘.
  • Rotationen eines Kreises können als kommutative kontinuierliche Symmetriegruppe betrachtet werden. Im Gegensatz dazu ist die Symmetriegruppe der Erdkugel nicht kommutativ: Wenn man vom Äquator ausgeht, der durch Afrika verläuft, führt eine Drehung nach links und dann nach unten nicht zu demselben Ergebnis wie eine Drehung nach unten und dann nach links. Im ersten Fall schaut man am Ende auf den Südpol, im zweiten Fall auf den Äquator auf der westlichen Hemisphäre, wobei die Pole nun horizontal liegen.
  • Nicht-kommutative Symmetriegruppen wurden bisher durch nicht-kommutative Matrizen dargestellt, d. h. durch Matrizen, bei denen die Reihenfolge der Operationen das Endergebnis beeinflusst. Dies ermöglicht jedoch keine geometrische Interpretation, da die Geometrie der nicht-kommutativen Algebren noch nicht gut verstanden ist. Andererseits können kommutative Algebren durch ihre Geometrie gut verstanden werden.
  • Eine „große Algebra“ ist eine kommutative ‚Übersetzung‘ einer nicht-kommutativen Matrix-Algebra, und gibt somit Zugang zu algebraischen Geometrietechniken. Große Algebren ermöglichen es also, neues Licht auf die Eigenschaften nicht-kommutativer kontinuierlicher Symmetriegruppen zu werfen.

Man könnte die Mathematik, die genaueste aller wissenschaftlichen Disziplinen, als die ultimative Suche nach der absoluten Wahrheit betrachten. Allerdings müssen auf dem mathematischen Weg zur Wahrheit oft gewaltige Hindernisse überwunden werden, ähnlich wie bei der Eroberung unvorstellbar hoher Berggipfel oder dem Bau riesiger Brücken zwischen isolierten Kontinenten. Die mathematische Welt ist voller Geheimnisse, und mehrere mathematische Disziplinen haben sich auf verschlungenen Pfaden und in völliger Isolation entwickelt. Um eine unumstößliche Wahrheit über komplexe Phänomene in der physikalischen Welt zu finden, bedarf es daher der Intuition und eines hohen Maßes an Abstraktion. Selbst grundlegende Aspekte der Physik treiben die Mathematik zu neuen Gipfeln der Komplexität. Dies gilt insbesondere für Symmetrien, mit deren Hilfe Physiker:innen einen ganzen Zoo subatomarer Teilchen, aus denen unser Universum besteht, theoretisiert und entdeckt haben.

In einem außergewöhnlich ehrgeizigen Unterfangen hat Tamás Hausel, Professor am Institute of Science and Technology Austria (ISTA), ein neues mathematisches Werkzeug namens „big algebras“ (große Algebren) nicht nur vermutet, sondern auch bewiesen. Dieses neue Theorem wirkt ähnlich wie ein ‚Wörterbuch‘, das die abstraktesten Aspekte der mathematischen Symmetrie mit Hilfe der algebraischen Geometrie entschlüsselt. Indem sie an der Schnittstelle von Symmetrie, abstrakter Algebra und Geometrie operieren, nutzen die großen Algebren greifbarere geometrische Informationen, um anspruchsvolle mathematische Eigenschaften über Symmetrien zu rekapitulieren. „Mit großen Algebren können uns Informationen von der ‚Spitze des mathematischen Eisbergs‘ ungeahnte Einblicke in die verborgenen Tiefen der mysteriösen Welt der Symmetriegruppen geben“, sagt Hausel. Mit diesem mathematischen Durchbruch will Hausel die Verbindung zwischen zwei weit voneinander entfernten Bereichen der Mathematik festigen: „Stellen Sie sich einerseits eine Welt der mathematischen Darstellungen der Quantenphysik vor und andererseits, sehr, sehr weit entfernt, die rein mathematische Welt der Zahlentheorie. Mit der vorliegenden Arbeit hoffe ich, dem Bau einer stabilen Verbindung zwischen diesen beiden Welten einen Schritt näher gekommen zu sein.“

Eine mathematische Übersetzung in beide Richtungen

Im 17. Jahrhundert zeigte uns der Philosoph und Mathematiker René Descartes, dass wir die Geometrie von Objekten mit Hilfe algebraischer Gleichungen verstehen können. Damit war er der erste, der mathematische Informationen zwischen diesen ehemals getrennten Bereichen ‚übersetzte‘. „Ich betrachte die Beziehungen zwischen verschiedenen mathematischen Bereichen gerne als Wörterbücher, die Informationen zwischen oft nicht gegenseitig verständlichen mathematischen Sprachen übersetzen“, sagt Hausel. Bislang wurden mehrere solcher mathematischen ‚Wörterbücher‘ entwickelt, aber einige übersetzen die Informationen nur in eine Richtung, während der ‚Rückweg‘ verborgen bleibt. Außerdem ist der Begriff „Algebra“ heutzutage komplexer geworden: er umfasst sowohl die klassische Algebra, wie zu Descartes‘ Zeiten, als auch die abstrakte Algebra – das Studium mathematischer Strukturen, die nicht unbedingt mit Zahlenwerten ausgedrückt werden können. Nun verwendet Hausel die abstrakte Algebra und die algebraische Geometrie wie ein ‚Wörterbuch‘, das in beiden Richtungen übersetzt.

Ein Skelett und Nervensystem

Mathematisch wird die Symmetrie als eine Art ‚Invarianz‘ definiert. Unter „Symmetriegruppe“ versteht sich die Gruppe aller Transformationen, die diese Unveränderlichkeit bewahren. Symmetriegruppen werden als ‚kontinuierlich‘ (z.B., die Drehung eines Kreises oder einer Kugel), oder ‚diskret‘ (z.B., die Spiegelung eines Objekts) eingestuft. Kontinuierliche Symmetriegruppen werden durch Matrizen – rechteckige Zahlenreihen – mathematisch dargestellt. Ausgehend von einer Matrixdarstellung einer kontinuierlichen Symmetriegruppe, kann Hausel die große Algebra berechnen und ihre wesentlichen Eigenschaften geometrisch darstellen, indem er ihr ‚Skelett‘ und ‚Nervensystem‘ auf einer mathematischen Oberfläche zeichnet. Das Skelett und Nervensystem der großen Algebra führen zu interessanten 3D-druckbaren Formen, die anspruchsvolle Aspekte der ursprünglichen mathematischen Information rekapitulieren und so den Übersetzungskreis schließen. „Ich bin von dieser Arbeit besonders begeistert, da sie uns einen völlig neuen Ansatz bietet, um die Darstellungen kontinuierlicher Symmetriegruppen zu untersuchen. Bei großen Algebren funktioniert die mathematische ‚Übersetzung‘ nicht nur in eine Richtung, sondern in beide.“

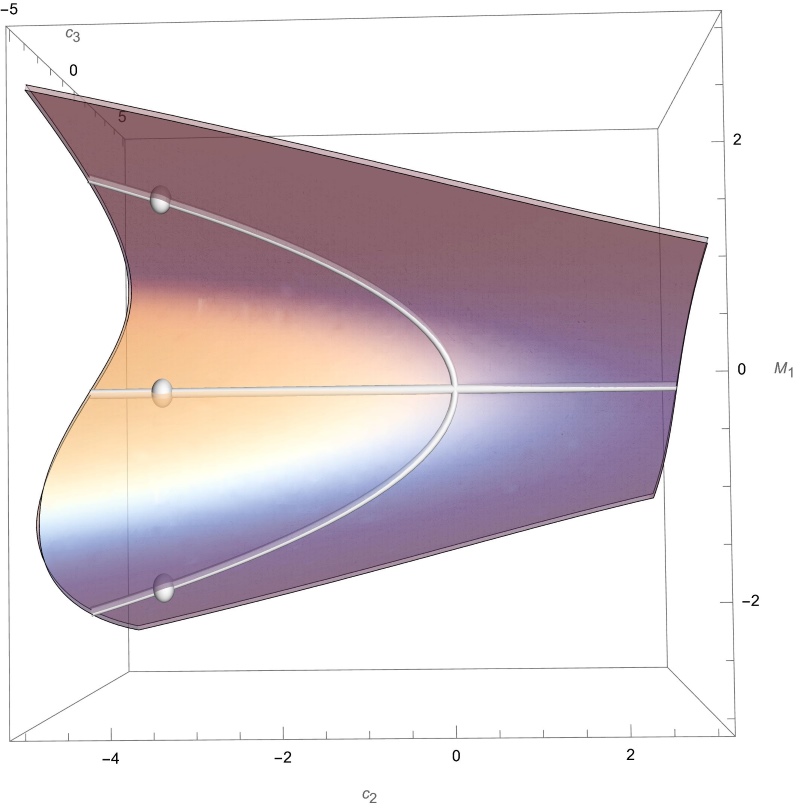
Brückenschlag zwischen isolierten Kontinenten in einer riesigen Welt der Mathematik

Wie könnten große Algebren die Verbindung zwischen Quantenphysik und Zahlentheorie stärken, zwei Bereichen der Mathematik, die scheinbar Welten voneinander entfernt sind? Erstens macht die Mathematik hinter der Quantenphysik ausgiebig Gebrauch von Matrizen. Diese Matrizen sind jedoch in der Regel ‚nicht kommutativ‘, d. h. die Multiplikation der ersten Matrix mit der zweiten führt nicht zum selben Ergebnis wie die Multiplikation der zweiten mit der ersten. Dies stellt ein Problem auf der Ebene der Algebra und der algebraischen Geometrie dar, da die nicht-kommutative Algebra noch nicht gut verstanden wird. Große Algebren lösen nun dieses Problem: Eine große Algebra ist eine kommutative ‚mathematische Übersetzung‘ einer nicht-kommutativen Matrixalgebra. So können die ursprünglich in nicht-kommutativen Matrizen enthaltenen Informationen entschlüsselt und geometrisch dargestellt werden, um ihre verborgenen Eigenschaften zu enthüllen.

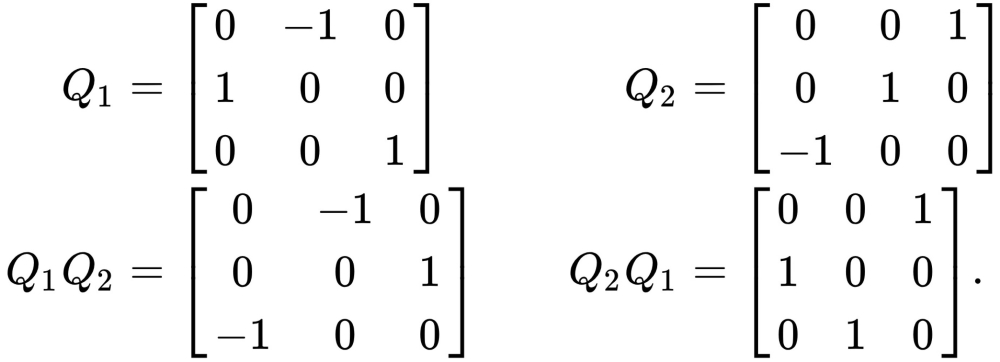
Zweitens zeigt Hausel, dass große Algebren nicht nur Beziehungen zwischen verwandten Symmetriegruppen aufzeigen, sondern auch, wenn ihre so genannten „Langlands-Duale“ verwandt sind. Diese Duale sind ein zentrales Konzept in der rein mathematischen Welt der Zahlentheorie. Im Langlands-Programm, einem hochkomplexen, groß angelegten Wörterbuch, das versucht, isolierte mathematische ‚Kontinente‘ zu überbrücken, ist die Langlands-Dualität ein Konzept oder Werkzeug, das die ‚Abbildung‘ mathematischer Informationen zwischen verschiedenen Kategorien ermöglicht. „In meiner Arbeit scheinen große Algebren verschiedene Symmetriegruppen genau dann miteinander zu verbinden, wenn ihre Langlands-Duale miteinander verwandt sind – ein recht überraschendes Ergebnis mit möglichen Anwendungen in der Zahlentheorie“, sagt Hausel.

„Idealerweise würden große Algebren es mir ermöglichen, die Langlands-Dualität in der Zahlentheorie mit der Quantenphysik zu verbinden“, sagt Hausel. Bislang konnte er zeigen, dass große Algebren zentrale Probleme auf beiden Kontinenten lösen. Der Nebel beginnt sich zu lichten, und die Kontinente der Quantenphysik und der Zahlentheorie haben einen Blick auf die Berge und Küsten des jeweils anderen am Horizont erhascht. Anstatt die turbulente mathematische Meerenge, die die Kontinente trennt, nur mit dem Schiff zu verbinden, könnte bald eine solide Brücke aus großen Algebren die anspruchsvolle Überquerung erleichtern.

Publikation:

Hausel T. 2024. Commutative avatars of representations of semisimple Lie groups. Proceedings of the National Academy of Sciences of the USA (PNAS). DOI: 10.1073/pnas.2319341121

Projektförderung:

Dieses Projekt wurde durch Mittel aus dem Österreichischen Wissenschaftsfonds (FWF), Projektförderung „Geometry of the tip of the global nilpotent cone“ no. P 35847, finanziert.