Jahrzehnte alte Erdős-Vermutung geknackt

Einige der berühmtesten Probleme der Mathematik bleiben für Jahrhunderte ungelöst. Für Erdős‘ Vermutung dauerte es fünfzig Jahre, bis eine Lösung gefunden wurde. Professor Matthew Kwan vom Institute of Science and Technology Austria (ISTA) und Mathematiker aus Harvard und dem MIT präsentieren einen Beweis, der die Existenz sogenannter Steiner-Tripelsystemen mit hoher Taillenweite belegt.

Als Matthew Kwan während seines Studiums von der Erdős-Vermutung hörte, hätte er niemals gedacht, ein paar Jahre später den Beweis dieses berüchtigten Theorems zu präsentieren. In der neuen Arbeit beweisen Kwan und Kollegen die Existenz von Steiner-Tripelsystemen mit beliebig hoher Taillenweite (engl. high-girth). Für den ausgefeilten Beweis arbeitete das neue ISTA-Fakultätsmitglied Kwan mit dem Kollegen Michael Simkin der Harvard University und den beiden Ausnahmestudenten Ashwin Sah und Mehtaab Sawhney vom Massachusetts Institute of Technology (MIT) zusammen.

Steiner‘sche Tripelsysteme sind grundlegende Typen von kombinatorischen Designs, die ihre Wurzeln im Entwerfen von Experimenten haben. So ist es beispielsweise wichtig zu wissen, welche Getreidesorten auf Böden mit unterschiedlichen Eigenschaften gedeihen können. Wie kann man aber alle Kombinationen effizient testen? Mit geschickter Kombinatorik lässt sich die Zahl der Experimente wesentlich reduzieren. Heutzutage untersucht die kombinatorische Designtheorie abstraktere Zusammenhänge. Ihre Resultate sind für die Theorien hinter Computercode relevant. Nach wie vor sind jedoch grundlegende Probleme ungelöst. Dazu gehörte auch die Erdős-Vermutung – bis jetzt.

Was ist die Erdős-Vermutung?

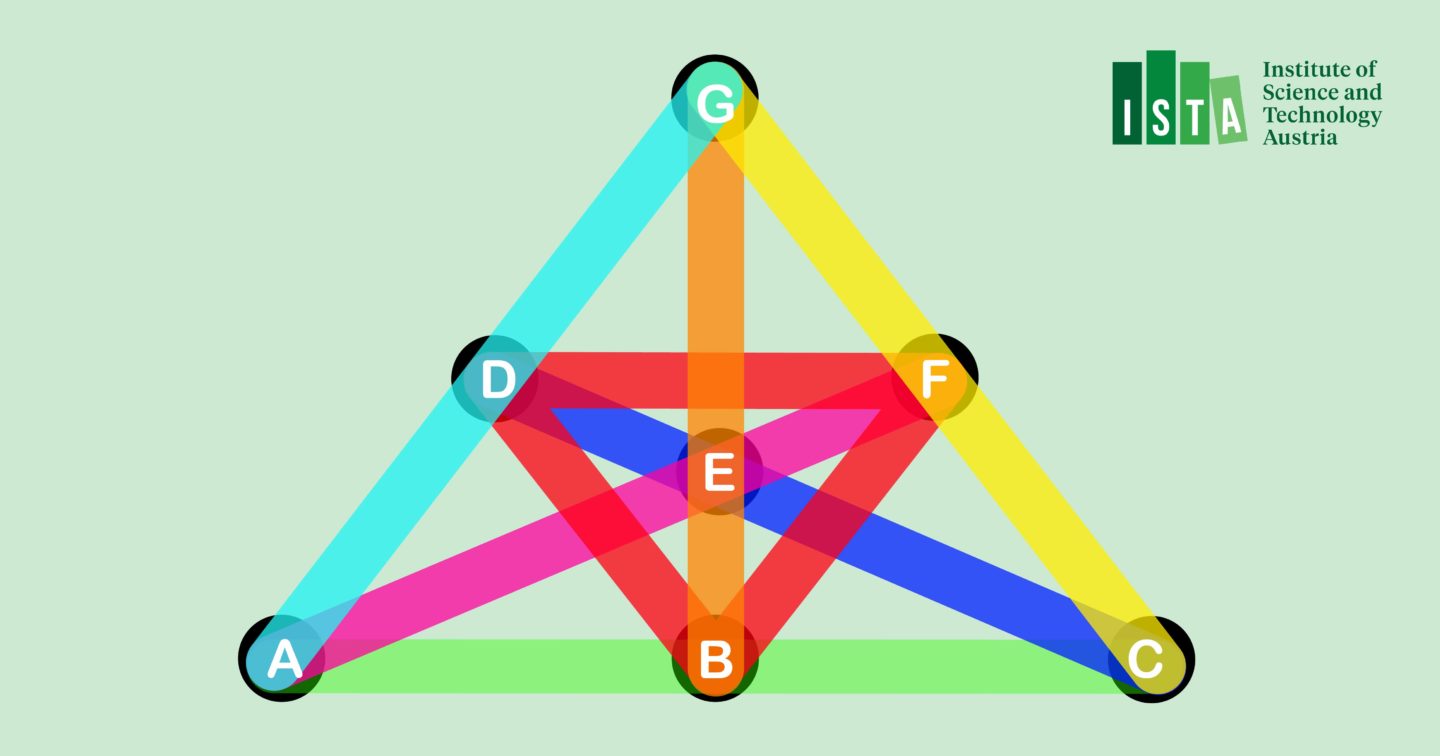
Die Vermutung bezieht sich auf so genannte Steiner-Tripelsysteme. Angenommen, sieben Personen wollen Dreiergruppen bilden. Jede Person kann Teil mehrerer Tripel sein, aber jedes Personenpaar darf nur Teil von exakt einer Dreiergruppe sein. Ein Individuum A kann daher Teil von drei Tripeln sein, indem es das erste Tripel mit B und C, das zweite mit E und F und das dritte mit D und G bildet. B zum Beispiel darf kein Trio mehr bilden, das A oder C enthält, da die Paare BA und BC schon im Tripel ABC vorkommen. B kann aber immer noch zwei andere Tripel bilden. Tatsächlich sind bei sieben Personen – oder Punkten, wie sie in Designs genannt werden – genau sieben Tripel möglich. In diesem Beispiel liegt ein Steiner-Tripelsystem vor.

Die Mathematiker zeigten, dass Steiner-Tripelsysteme mit der wünschenswerten Eigenschaft einer hohen Taillenweite tatsächlich existieren. Eine hohe Taillenweite ist eine statistische Bedingung. Wenn sich viele Tripel über eine kleine Anzahl von Punkten erstrecken, ist die Taillenweite niedrig. „Solche dichten Stellen treten bei algebraischen Konstruktionen unweigerlich auf“, erklärt Kwan. „Erdős hat sich gefragt, ob man sie vermeiden kann. Wenn Tripel keine solchen Konfigurationen aufweisen, sagt man, dass das System eine hohen Taillenweite besitzt. Um ihre Existenz zu beweisen, muss man die Algebra vermeiden und Methoden aus der Wahrscheinlichkeitstheorie, der Probabilistik, einführen. Das ist uns gelungen.“

Interdisziplinarität innerhalb der Mathematik

In Designtheorie, diesem vielleicht ältesten Gebiet der Kombinatorik gab es bis vor acht Jahren nur begrenzte Fortschritte bei den fundamentalen Fragen. Kwans Hintergrund in probabilistischer Kombinatorik eröffnete ihm die Vorstöße, die das Gebiet seit den bahnbrechenden Fortschritten im Jahr 2014 revolutionierten. Der neue Beweis umfasst eine breite Palette von Techniken an der Grenze zwischen extremaler und probabilistischer Kombinatorik. „Zusätzlich haben wir zwei neue Methoden benutzt: Die Retrospektive Analyse, die es uns ermöglicht, die Zufälligkeit in früheren Schritten nachzuverfolgen, und Sparsification, eine Art Ausdünnung, die alle Herausforderungen der retrospektiven Analyse beseitigt“, fasst Kwan die technischen Aspekte des Ergebnisses zusammen.

Mit seiner Gruppe am ISTA strebt Kwan ein besseres Verständnis der Grundlagen von mathematischen Designs an, insbesondere unter dem Gesichtspunkt der Wahrscheinlichkeitstheorie. „Meine Philosophie: Ich versuche, an verschiedenen Dingen zu arbeiten. Es mag verlockend sein, sich komplett auf ein Teilgebiet zu konzentrieren, aber wenn man sein ganzes Leben lang an verschiedenen Problemen tüftelt, findet man jene Techniken, die einem helfen, in anderen Bereichen Neues zu entdecken.“

Publikation:

Kwan E, Sah A, Sawhney M und Simkin M. 2022. High-girth Steiner triple systems. Preprint. arXiv:2201.04554v3

Weitere Lektüre

Erica Klarreich (2015): A Design Dilemma Solved, Minus Designs. Quanta Magazine. – Populäre Darstellung der Steiner Tripelsysteme und der jüngsten Durchbrüche in der Designtheorie.

Yufei, Zhao (2022): Kwan-Sah-Sawhney-Simkin: High-girth Steiner triple systems. – Detaillierter Blog-Eintrag.