Die ganze Mathematik in einer Datenbank?

„Mathematik“ ist ein Oberbegriff, der verschiedene Teilgebiete mit unterschiedlichen Konventionen vereint. Wenn man mathematische Sätze beweisen will, ist es fast unmöglich, das gesamte mathematische Wissen zu berücksichtigen. Außerdem ist das Peer-Review-Verfahren notorisch langsam. Martin Dvořák, PhD Student in der Kolmogorov Gruppe am Institute of Science and Technology Austria (ISTA), ist auch Mathlib-Entwickler—eine Software, die mathematische Konzepte digitalisiert und zentralisiert. Erfahren Sie mehr über sein „Nebenprojekt“.

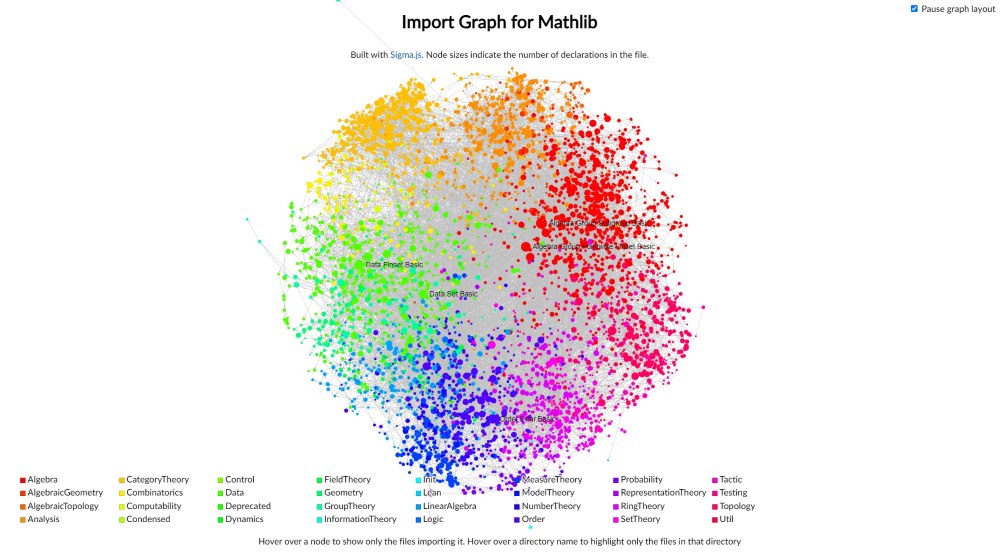
Die ganze Mathematik in eine Art Bibliothek von Alexandria des 21.Jahrhunderts zusammenzufügen? Das ist das kollektive Bestreben einer kleinen weltweiten Gemeinschaft von akribischen Mathematiker:innen. Sie haben die Vision, eines Tages das gesamte mathematische Wissen der Menschheit über alle Teilgebiete hinweg zu zentralisieren. Neben der Archivierung revolutioniert diese akribische Ameisenarbeit die Mathematik und macht mathematische Entdeckungen für die künstliche Intelligenz (KI) zugänglich.

Diese neue Bibliothek von Alexandria, die die gesamte Mathematik umfassen wird, ist eine Computersoftware namens „Mathlib“. Sie zentralisiert Konzepte, die in allen mathematischen Teilgebieten wahr sind, und macht sie zur Grundlage der „Wahrheit“ für alle künftigen Einträge. Geboren aus „Lean“, einer „schlanken“ (so der Name), effizienten und übersichtlichen Programmiersprache für die Softwareentwicklung, die 2013 eingeführt wurde, steht Mathlib für „Lean mathematical library“ (Schlanke mathematische Bibliothek). „Lean ist die Code-Sprache der Logik und Mathlib ist die Bibliothek, die auf dieser Logik aufbaut“, erklärt Doktorand Martin Dvořák.

Der junge Forscher ist derzeit sowohl am Institute of Science and Technology Austria (ISTA) als auch in Österreich der einzige Mathlib-Entwickler. „Meine Leidenschaft ist es, dabei zu helfen, die gesamte Mathematik zu digitalisieren, um so dessen Fortschritt voranzutreiben. Dieses ‚Nebenprojekt‘ hilft mir natürlich auch bei meiner Routine als Doktorand, in der ich Theoreme (Sätze) beweise. Dank der enormen Hilfe von Mathlib, führe ich alle meine Satz-Beweise interaktiv in Lean durch. Je mehr Lemmata – also Zwischensätze – in Mathlib enthalten sind, desto weniger muss ich Theoreme von Grund auf beweisen.“

„Schlanke“ Logik: vom Softwarecode bis zum mathematischen Beweis

Als Lean auf den Markt kam, erkannten Mathematiker:innen schnell, dass die Art, wie Lean die Gültigkeit von Softwarecode überprüfen kann, einem mathematischen Beweis ähnelt. Diese Gelegenheit konnten die Forschenden sich nicht entgehen lassen. Ihr Bedarf an einer neuen, gut geplanten und sorgfältig aufgebauten mathematischen Bibliothek war viel zu real.

Computergestützte Beweishilfen sind aber nichts Neues. Das erste Programm dieser Art, „Automath“, wurde in den 1960er Jahren eingeführt. Es folgten „Mizar“ im Jahr 1973 und „Coq“ im Jahr 1989, zwei Beweisassistenten, die unter Mathematiker:innen weit verbreitet waren. Doch, anstatt dass sie das mathematische Wissen in Coq zentralisieren, definierten seine Benutzer:innen unabhängig voneinander Probleme, die nur sie interessierten, und verwendeten dabei oft eine eigene Sprache. Dies führte dazu, dass Coq wie eine ungeplante Stadt gewachsen ist, wobei die vielen kleineren, unabhängigen Bibliotheken die Plattform unübersichtlich machten. Lean verschaffte den Mathematiker:innen einen dringend benötigten Neuanfang, bei dem sie aus vergangenen Herausforderungen schöpfen konnten. „Lean ermöglichte es, dass wir uns gemeinsam auf eine Interpretation der von Menschen geschriebenen Mathematik einigen konnten. Mit diesem Werkzeug können wir Konzepte entwickeln, die unter allen Umständen wahr bleiben, und sie eindeutig in einer Computersoftware kodieren, die für alle zugänglich ist“, so Dvořák. Auf diese Weise arbeitet die „Lean Community“ von Entwickler:innen am Aufbau von Mathlib. Das Fundament wird Stein für Stein aufgebaut.

Eine kugelsichere Pyramide der Beweise

Dvořák und seine Mathlib-Entwicklerkolleg:innen auf der ganzen Welt bauen also eine solide Grundlage für die Mathematik auf. Ausgehend von spezifischen Problemen in einem Teilgebiet der Mathematik suchen sie nach den allgemeinsten und am breitesten anwendbaren Versionen mathematischer Konzepte. Das Beweisen von Theoremen in Lean ist ein interaktiver Prozess zwischen dem Entwickler oder der Entwicklerin und dem Computer, erklärt Dvořák. Der Entwickler oder die Entwicklerin gibt immer mehr Hinweise, wie ein Konzept verifiziert werden soll, und die Software ermittelt es auf der Grundlage der bereits verifizierten Elemente. Die Mathlib-Entwickler:innen extrahieren auch mathematische Denkmuster und kodieren sie als „Taktiken“ – logische Bausteine – in Lean.

Mathlib funktioniert also wie eine Pyramide der Beweise. Abgesehen davon, dass Mathlib logisch kugelsicher ist, ist die Bibliothek auch sehr agil. „Unsere Aufgabe als Entwickler:innen ist es, dafür zu sorgen, dass die Pyramide eine solide, aber flexible Basis hat. Wenn man einen neuen ‚Stein‘ in Mathlib hinzufügt, kann der PC die gesamte Pyramide über Nacht neu erschaffen, alles auseinandernehmen und ein Baustein nach dem anderen neu aufbauen“, erklärt Dvořák. Dadurch wird sichergestellt, dass alles vom Computer auf mathematische Korrektheit überprüft wird. Wenn also ein Benutzer oder eine Benutzerin – ob Mensch oder KI (z.B. AlphaProof von Google DeepMind) – ein Problem zusammen mit Anweisungen zum Beweisen eingibt, kann Mathlib schnell die notwendigen Prüfungen durchführen und einen computergenerierten Beweis liefern.

In die Zukunft der Mathematik investieren

Große mathematische Ergebnisse hängen von Hunderten von mathematischen Publikationen ab. Das menschliche Versagen macht es aber unmöglich, sicherzustellen, dass die Argumentation durchgehend korrekt ist. „Wenn Sie Ihre Beweise auf Lemmata in Mathlib stützen, haben Sie die höchste Garantie, dass alles, was Sie verwenden, am Computer auf absolute Korrektheit überprüft wurde“, führt Dvořák fort.

Mathlib macht nicht nur mathematische Beweise kugelsicher, sondern demokratisiert auch die Mathematik. Sie fördert die Zusammenarbeit zwischen Mathematiker:innen und überwindet wichtige Barrieren des wissenschaftlichen „Vertrauens“ in diesem Bereich. „Mathlib kann Ihnen innerhalb von fünf Sekunden sagen, ob Sie einen eklatanten Fehler in Ihrer Argumentation gemacht haben. Das spart unglaublich viel Zeit, wenn man das mit dem monatelangen Warten auf ein menschliches Peer-Review vergleicht“, so Dvořák. „Andererseits ist es sehr befriedigend, wenn der Computer die Nachricht ‚goals accomplished‘ anzeigt. Dann weiß man, dass niemand mehr widerlegen kann, was man eben bewiesen hat.“

Dvořák ist sichtlich stolz auf seinen Beitrag zu diesem kolossalen Gemeinschaftswerk, aber er ist sich sehr wohl bewusst, dass Mathlib, eben wie die Mathematik, nie „fertig“ sein kann. „Wir wissen nicht, wie die Mathematik in ein paar Jahrzehnten aussehen wird. Tatsächlich kennen wir nicht einmal das Ausmaß des mathematischen Wissens der Menschheit in diesem Augenblick. Aber ich bin überzeugt, dass sich unsere Ameisenarbeit in einer Weise auszahlen wird, die wir uns heute noch gar nicht vorstellen können.“